Introduction to Statistical Testing and ANOVA

Hypothesis testing is a cornerstone of quantitative research, and even as you progress in statistical expertise, certain foundational steps—such as examining descriptive statistics and data management—remain essential. In testing hypotheses, selecting the appropriate statistical tool depends on the type of variables involved. For instance, when dealing with a categorical explanatory variable (e.g., presence or absence of depression) and a quantitative response variable (e.g., number of cigarettes smoked), the Analysis of Variance (ANOVA) is the tool to use. ANOVA evaluates whether the means of the response variable differ significantly across the categories of the explanatory variable.

How ANOVA Works: Comparing Means

The core idea behind ANOVA lies in comparing means across groups defined by the explanatory variable. The ANOVA F-test determines whether the observed differences in sample means reflect true differences in population means or if they could have occurred due to random variability. For example, consider a study investigating whether academic frustration levels differ across college majors. In this scenario:

• Explanatory Variable (X): College major (e.g., Business, English, Mathematics, Psychology).
• Response Variable (Y): Level of academic frustration, rated on a scale of 1 to 20.

The null hypothesis (H0H_0H0​) states that there is no relationship between the explanatory and response variables, implying that all group means are equal (μ1=μ2=μ3=μ4\mu_1 = \mu_2 = \mu_3 = \mu_4μ1​=μ2​=μ3​=μ4​). Conversely, the alternative hypothesis (HaH_aHa​) asserts that not all group means are equal.

Examining Sample Data: Means and Variation

Using random samples of 35 individuals from each major, the mean frustration scores were as follows:

• Business: 7.3
• English: 11.8
• Mathematics: 13.2
• Psychology: 14.0

While differences in sample means are evident, the key question is whether these differences are statistically significant. To answer this, ANOVA assesses two types of variation:

1. Variation Among Sample Means: How far apart the group means are from each other.
2. Variation Within Groups: How much individual data points vary within each group.

The F statistic, which forms the basis of ANOVA, is calculated as the ratio of these two variations: F=Variation Among Sample MeansVariation Within GroupsF = \frac{\text{Variation Among Sample Means}}{\text{Variation Within Groups}}F=Variation Within GroupsVariation Among Sample Means​

When the variation among sample means is large relative to the variation within groups, the F statistic will be high, providing stronger evidence against the null hypothesis.

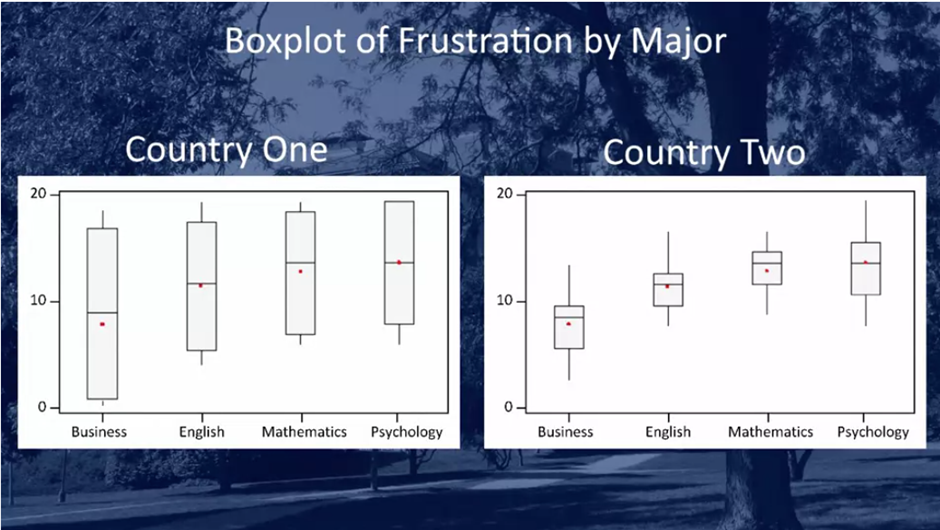
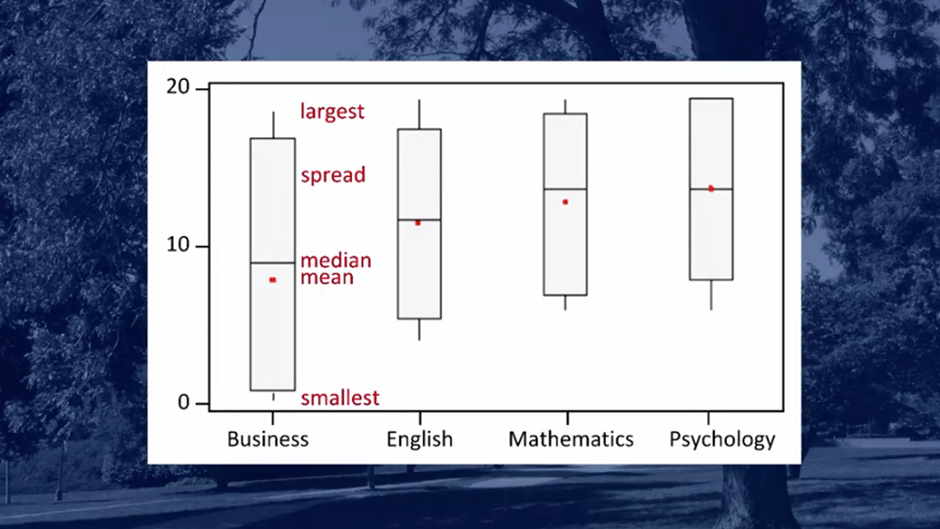
Boxplot Illustration of Variation

Boxplots visually represent the variation within and among groups. Consider two hypothetical datasets:

• Dataset 1 (Country One): High variation within groups, leading to overlapping frustration scores among majors. This could indicate that any observed differences in means might arise by chance, supporting the null hypothesis.
• Dataset 2 (Country Two): Low variation within groups, with minimal overlap in frustration scores. Here, differences in means are more likely due to true differences in population means, supporting the alternative hypothesis.

The extent of overlap in boxplots highlights the relationship between group variability and evidence against the null hypothesis.

Results of the ANOVA F-Test

For Dataset 2 (Country Two), the ANOVA F statistic was calculated as 46.60, indicating that the variation among sample means was much greater than the variation within groups. The corresponding p-value was practically 0 (e.g., 0.0001). This tiny p-value suggests it is extremely unlikely to observe data like this if the null hypothesis were true. Specifically:

• There is a 0.01% chance of incorrectly rejecting the null hypothesis (Type I Error).
• There is a 99.99% confidence in accepting the alternative hypothesis.

Thus, the null hypothesis is rejected, and it is concluded that there is a significant association between academic frustration levels and college major. In other words, frustration levels vary significantly across majors.

Conclusion and Application

The ANOVA F-test provides a robust method for analyzing differences in means across groups. By comparing variation among and within groups, it determines whether observed differences are statistically significant. The example demonstrates how ANOVA can reveal meaningful relationships in data, such as the association between academic frustration and college major. Moving forward, this understanding can be applied to other datasets, and statistical tools like SAS can be used to automate these analyses efficiently.